Um ein analoges Signal wie z.B. einen Sinus zu erzeugen, benötigt man einen Digital-Analog-Wandler (DAC) .
| eine analogen
Eingangsspannung von 0V ... 5V wird gemessen und damit
die Frequenz eines Sinus im Bereich von 0Hz ... 3200 Hz gesteuert. Um ein analoges Signal wie z.B. einen Sinus zu erzeugen, benötigt man einen Digital-Analog-Wandler (DAC) . |
 |
Schaltung
 |
Die Schaltung besteht aus einem PIC16F876
(oder anderer
16F87x),
einer 20-MHz-Taktquelle für den PIC (z.B. Quarz) und
einem DAC mit R/2R-Widerstandsnetzwerk (gelb hinterlegt). Die
analoge Spannung wird an RA0 ind den PIC gespeist (z.B. von einem
Potentiometer). Der Sinus steht am
Ausgang des DAC zur Verfügung. Zum Aufbau eignet sich z.B. die 16F876-Testplatine, mit der Analogeingangsplatine am Port
A und einer R/2R-DAC-Platine
(hier nochmal als Testplatine)
am Port B. Am Ausgang wird ein Sinussignal ausgegeben, dessen Frequenz im
Bereich von 0 Hz bis 3,2 kHz durch die Spannung am Pin RA0 bestimmt
wird. Um das erzeugte Signal sichtbar zu machen, ist ein Oszilloskop ideal. Dafür sind die blau hinterlegten Schaltungsteile dann unnötig und können entfallen. Wenn man aber kein Oszilloskop hat, kann man an den Ausgang eine Reihenschaltung aus einem 100-nF-Kondensator (darf auch gern deutlich größer sein) und einem Kopfhöher anschließen. (blau hinterlegter optionaler Schaltungsteil) Für PCs gibt es "Oszilloskopsoftware", die die
Soundhardware des PC als Analogeingang benutzt. Um den DAC an den
Line-In-Eingang des PC anzuschließen, sind ein Kondensator (darf
auch deutlich größer als 100nF sein) und
ein Widerstandsspannungsteiler nötig. (ebenfalls blau hinterlegter
optionaler Schaltungsteil) |
ADC
Der ADC wurde bereits
mehrfach ausführlich
behandelt.
Er
wird
hier
benutzt,
um
den
Pegel der Spannung am Pin RA0 (0 .. 5V) zu messen. Dazu
wird der
ADC am Programmanfang so eingestellt, dass er die Spannung an RA0 misst
und rechtsbündig in seine Ergebnisregister schreibt.
Später wird in der Sinus-Endlosschleife immer wieder getestet, ob der ADC mit einer Messung fertig ist. Ist das der Fall, dann wird der Messwert als Frequenz (f1 & f1+1) in das Programm übernommen und der ADC erneut gestartet. Liegt kein Messwert vor, dann geht das Programm in eine kleine Verzögerungsroutine, die genau so lange dauert, wie die Übernahme der Messwerte gedauert hätte. Das garantiert, dass jede Sinus-Schleife gleich lang ist.
| ... ... ; ADC vorbereiten ; ADC einschalten BSF ADCON0, 0 ; ADON=1 ; ADC-Eingang AN0 auswählen BCF ADCON0, 5 ; ADCHS2=0 BCF ADCON0, 4 ; ADCHS1=0 BCF ADCON0, 3 ; ADCHS0=0 ; ADC speed für 20 MHz einstellen BSF ADCON0, 7 ; ADCS1=1 BCF ADCON0, 6 ; ADCS0=0 ; Daten linksbündig BSF STATUS,RP0 ; Bank1 BCF ADCON1, 7 ; ADFM=0 BCF STATUS,RP0 ; Bank0 BSF ADCON0, 2 ; ADC starten ... ... ... _next ... ... ... BTFSC ADCON0, 2 ; ist der ADC fertig? GOTO _del ; nein, weiter warten movfw ADRESH ; obere 2 Bit auslesen movwf f1+1 ; obere 2 Bit nach f1+1 BSF STATUS,RP0 ; Bank1 movfw ADRESL ; untere 8 Bit auslesen BCF STATUS,RP0 ; Bank0 movwf f1 ; untere 8 Bit nach f1 BSF ADCON0, 2 ; ADC starten goto _next _del nop nop nop nop nop nop goto _next ... ... |
DAC
Ein DAC (digital-analog-converter) wandelt einen Zahlenwert in eine Spannung. Der Spannungspegel ist dabei dem Zahlenwert proportional. PIC-Controler haben keine integrierte DAC-Hardware, und so muss man einen DAC als externe Baugruppe anschließen. Ich habe mich hier für einen DAC mit R/2R-Widerstandsmatrix entschieden, da dieser schnell ist und sich in ein paar Minuten zusammenlöten lässt.
Sinus
Um einen Sinus mit dem DAC auszugeben, muss man den DAC-Eingang (PORTB) kontinuierlich mit Zahlenwerten beschreiben, die wertmäßig dem zeitlichen Verlauf des Sinus entsprechen. Da ein Sinus immer zwischen -1 und +1 pendelt, der DAC aber Eingangswerte zwischen 0 und 255 braucht, muss man die Sinuswerte noch etwas umrechnen, bevor man sie an den DAC weitergibt.| sine movlw 3 movwf PCLATH ; vorbereiten fuer Sin-Tabelle im Bereich 0x300..0x3ff _next ... ... ... movf akku+1,w call getsine ; w = sin(w) (Page 3) ; ca. 6 cyc movwf PORTB ; -> DAC ... ... ... goto _next ;**************************************************************************************** ; Sinustabelle aus 256 Werten ; Wert = (sin(w/256*2*Pi) + 1) *127.5 ; fuer w = 0 ...255 ; PCLATCH = 0x03 ; dadurch landet addwf im Bereich 3xxh org 2ffh getsine addwf PCL,f sintab DT 127,130,133,136,139,142,145,148 ; Anfang der positiven Halbwelle DT 151,154,157,160,163,166,169,172 DT 175,178,181,184,186,189,192,194 DT 197,200,202,205,207,209,212,214 DT 216,218,221,223,225,227,228,230 DT 232,234,235,237,238,240,241,243 DT 244,245,246,247,248,249,250,250 DT 251,252,252,253,253,253,253,253 DT 253,253,253,253,253,253,252,252 DT 251,250,250,249,248,247,246,245 DT 244,243,241,240,239,237,236,234 DT 232,230,229,227,225,223,221,219 DT 216,214,212,210,207,205,202,200 DT 197,195,192,189,187,184,181,178 DT 175,172,169,167,164,161,158,155 DT 151,148,145,142,139,136,133,130 ; Ende der positiven Halbwelle DT 127,124,120,117,114,111,108,105 ; Anfang der negativen Halbwelle DT 102, 99, 96, 93, 90, 87, 84, 81 DT 78, 75, 72, 70, 67, 64, 61, 59 DT 56, 54, 51, 49, 46, 44, 41, 39 DT 37, 35, 33, 31, 28, 27, 25, 23 DT 21, 19, 18, 16, 15, 13, 12, 11 DT 9, 8, 7, 6, 5, 4, 3, 3 DT 2, 1, 1, 0, 0, 0, 0, 0 DT 0, 0, 0, 0, 0, 0, 1, 1 DT 2, 3, 3, 4, 5, 6, 7, 8 DT 9, 10, 12, 13, 14, 16, 17, 19 DT 21, 22, 24, 26, 28, 30, 32, 34 DT 36, 39, 41, 43, 46, 48, 51, 53 DT 56, 58, 61, 64, 66, 69, 72, 75 DT 78, 80, 83, 86, 89, 92, 95, 98 DT 101,104,107,111,114,117,120,123 ; Ende der negativen Halbwelle end ;**************************************************************************************** |
Frequenzsteuerung durch den ADC
In der sine-Schleife des Programms wird immer wieder zum 16-Bit-Wert akku der 16-Bit-Wert f1 hinzuaddiert. Dadurch wird der Wert von akku immer größer, bis er 0xFFFF (65535) überschreitet. Dann beginnt alles von vorn. Die oberen 8 Bit von akku (akku+1) steigen im Wert folglich von 0 bis 255 an, um wieder (in etwa) bei 0 zu beginnen. Diese 8 Bit dienen als Index zum Auslesen der Sinustabelle.
Programmablauf
Spannung messen:
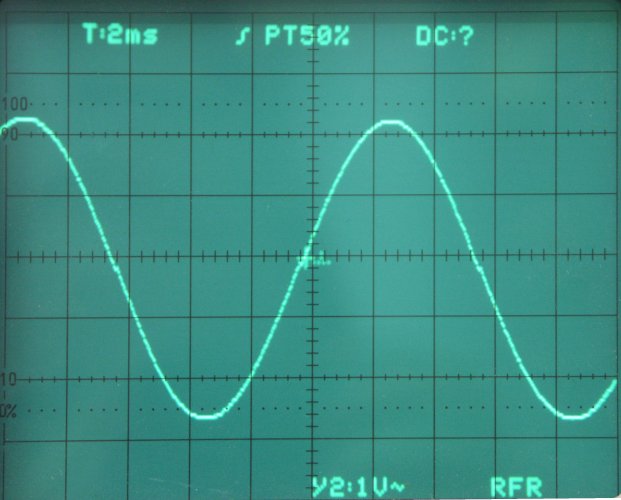
Ergebnis
Programmlisting
| list
p=16f876 ;************************************************************** ;* ;* Pinbelegung ;* ---------------------------------- ;* PORTA: 0 analoger Eingang ;* 1 - ;* 2 - ;* 3 - ;* 4 - ;* PORTB: 0 DAC ;* 1 DAC ;* 2 DAC ;* 3 DAC ;* 4 DAC ;* 5 DAC ;* 6 DAC ;* 7 DAC ;* PORTC: - ;* ;************************************************************** ; ; sprut (zero) Bredendiek 04/2010 ; ; ADC-DAC-Lernbeispiel: ; ; 16F876 wandelt die an RA0 anliegende Spannung in einen ; 10-Bit-Wert um ; die 10 Bit des Wertes steuern die Frequenz eines Sinusses ; der mit einem DAC am PORTB ausgegeben wird ; ; Prozessortakt: 20 MHz ; Eingangsspannung: 0V ... 5V (Vss ... Vdd) ; ;**************************************************************************************** ; ; im Quelltext wird mit dezimalen Zahlen gearbeitet list r=dec ;Set the radix as decimal. ; ;**************************************************************************************** ; Includedatei für den 16F876 einbinden #include <P16f876.INC> ;**************************************************************************************** ; Configuration festlegen: ; Power on Timer, kein Watchdog, HS-Oscillator, kein Brown out, kein LV-programming __CONFIG _PWRTE_ON & _WDT_OFF & _HS_OSC & _BODEN_OFF & _LVP_OFF ; clk = 20 MHz ; cycl = 5 MHz ;**************************************************************************************** ; Variablen cblock 0x20 akku:2 ;16 bit accumulator f1:2 ;16 bit frequenz endc ;**************************************************************************************** ; Startadresse org 0 start ; RA0 wird analoger input ; RB wird output fuer DAC bsf STATUS,RP0 ; Bank 1 movlw B'11111111' movwf TRISA clrf TRISB ; RB0..7 output bcf STATUS,RP0 ; Bank 0 clrf INTCON ; interrupts disabled clrf akku clrf akku+1 ; Phase = 0/65536 * 360grd movlw 1 movwf f1 clrf f1+1 ; Frequenz: f1 = 1 ; ADC vorbereiten ; ADC einschalten BSF ADCON0, 0 ; ADON=1 ; ADC-Eingang AN0 auswählen BCF ADCON0, 5 ; ADCHS2=0 BCF ADCON0, 4 ; ADCHS1=0 BCF ADCON0, 3 ; ADCHS0=0 ; ADC speed für 20 MHz einstellen BSF ADCON0, 7 ; ADCS1=1 BCF ADCON0, 6 ; ADCS0=0 ; Daten rechtsbündig BSF STATUS,RP0 ; Bank1 BSF ADCON1, 7 ; ADFM=1 BCF STATUS,RP0 ; Bank0 BSF ADCON0, 2 ; ADC starten goto sine ;**************************************************************************************** ; Erzeugung der Wellenform ;**************************************************************************************** ; Sinus ; frequenz: f1 ; benutzt Sinustabelle aus 256 Werten fuer eine Welle ; ca 24 zyklen pro loop ; f1 = 1 -> 24*256*256 zyklen -> 3,2 Hz ; f1 = 1023 -> 24* 64 zyklen -> 3200 Hz sine movlw 3 movwf PCLATH ; vorbereiten fuer Sin-Tabelle im Bereich 0x300..0x3ff _next movf f1,w addwf akku,f movf f1+1,w btfsc STATUS,C incfsz f1+1,w addwf akku+1,f ; akku = akku + f1 (16 Bit) movf akku+1,w call getsine ; w = sin(w) (Page 3) ; ca. 6 cyc movwf PORTB ; -> DAC BTFSC ADCON0, 2 ; ist der ADC fertig? GOTO _del ; nein, weiter warten movfw ADRESH ; obere 2 Bit auslesen movwf f1+1 ; obere 2 Bit nach f1+1 BSF STATUS,RP0 ; Bank1 movfw ADRESL ; untere 8 Bit auslesen BCF STATUS,RP0 ; Bank0 movwf f1 ; untere 8 Bit nach f1 BSF ADCON0, 2 ; ADC starten goto _next _del nop nop nop nop goto _next ;**************************************************************************************** ; Sinustabelle aus 256 Werten ; Wert = (sin(w/256*2*Pi) + 1) *127.5 ; fuer w = 0 ...255 ; PCLATCH = 0x03 ; dadurch landet addwf im Bereich 3xxh org 2ffh getsine addwf PCL,f sintab DT 126, 129, 132, 135, 138, 141, 144, 148 ; Anfang der positiven Halbwelle DT 151, 154, 157, 160, 163, 166, 168, 171 DT 174, 177, 180, 183, 185, 188, 191, 193 DT 196, 199, 201, 204, 206, 208, 211, 213 DT 215, 217, 219, 221, 223, 225, 227, 229 DT 231, 232, 234, 236, 237, 239, 240, 241 DT 242, 244, 245, 246, 247, 247, 248, 249 DT 250, 250, 251, 251, 251, 252, 252, 252 DT 252, 252, 252, 252, 251, 251, 251, 250 DT 250, 249, 248, 247, 247, 246, 245, 244 DT 242, 241, 240, 239, 237, 236, 234, 232 DT 231, 229, 227, 225, 223, 221, 219, 217 DT 215, 213, 211, 208, 206, 204, 201, 199 DT 196, 193, 191, 188, 185, 183, 180, 177 DT 174, 171, 168, 166, 163, 160, 157, 154 DT 151, 148, 144, 141, 138, 135, 132, 129 ; Ende der positiven Halbwelle DT 126, 123, 120, 117, 114, 111, 108, 104 ; Anfang der negativen Halbwelle DT 101, 98, 95, 92, 89, 86, 84, 81 DT 78, 75, 72, 69, 67, 64, 61, 59 DT 56, 53, 51, 48, 46, 44, 41, 39 DT 37, 35, 33, 31, 29, 27, 25, 23 DT 21, 20, 18, 16, 15, 13, 12, 11 DT 10, 8, 7, 6, 5, 5, 4, 3 DT 2, 2, 1, 1, 1, 0, 0, 0 DT 0, 0, 0, 0, 1, 1, 1, 2 DT 2, 3, 4, 5, 5, 6, 7, 8 DT 10, 11, 12, 13, 15, 16, 18, 20 DT 21, 23, 25, 27, 29, 31, 33, 35 DT 37, 39, 41, 44, 46, 48, 51, 53 DT 56, 59, 61, 64, 67, 69, 72, 75 DT 78, 81, 84, 86, 89, 92, 95, 98 DT 101, 104, 108, 111, 114, 117, 120, 123 ; Ende der negativen Halbwelle end ;**************************************************************************************** |
| procedure
TForm1.sinus; var w : real ; k, i : integer; st : string; begin memo1.lines.add('sintab'); st:=chr(9)+'DT'+chr(9); for k:=0 to 255 do begin w := sin(k/128*pi); i := round((w+1)*126); if (k mod 8) <> 0 then st := st+', '; if i<100 then st := st+' '; if i<10 then st := st+' '; st := st+inttostr(i); if (k mod 8) = 7 then begin memo1.lines.add(st); st:=chr(9)+'DT'+chr(9); end; end; memo1.lines.add(st); end; |
Mögliche Änderungen
Die Tabelle enthält 256 Sinuswerte. Zwischen zwei Werten liegt also ein Phasenabstand von 360 Grad/ 256 = 4,4 Grad . Das schränkt die Genauigkeit der Sinusfunktion ein. Eine bessere Auflösung lässt sich ohne größeren Speicherbedarf erreichen, wenn man mit den 256 Tabellenwerten nur das erste Viertel der Sinuswelle beschreiben würde. Der Abstand zwischen zwei Sinuswerten berüge dann nur 90 Grad/ 256 = 0,35 Grad .