Fast Fourier Transform (FFT)

Einleitung
FFT - kennt jeder
Die FFT als Filter-Bank
FFT ohne Mathematik erklärt
Signal-Rausch-Verhältnis
Frequenzen und Bandbreiten
Phasenmessung?
Komplexe Zahlen / IQ / Sinus & Cosinus
 

zurück zu DSP

Einleitung

Wer es exakt wissen will, kann ja mal auf www.wikipedia.de nach Schnelle Fourier-Transformation suchen, aber keinen Schreck von den Formeln bekommen.

Machen wir es uns mal einfach:
Die Grundschwingung ist bekanntlich die Sinusschwingung. Sie gilt als reine Schwingung, da sie nur eine einzelne Frequenz enthält. Andere Signale mögen zwar die gleiche Tonfrequenz haben, klingen aber trotzdem ganz anders. So klingt der selbe Kammerton 'a' (also die selbe Note) auf einer E-Gitarre ganz anders als auf einem Klavier oder einer Orgel. Das liegt daran, dass alle diese Töne aus der Grundfrequenz (in diesem Fall 440 Hz) sowie Mehrfachen dieser Frequenz (880 Hz, 1320 Hz, 1760 Hz) zusammengesetzt sind. Je nachdem, wie stark diese Mehrfachen (Oberwellen, Harmonische) sind, ergibt sich ein anderer Klang (ich ignoriere jeglich zusätzliche Amplitudenmodulation, um es einfach zu machen).
Wie Töne, besteht jede Signal-Schwingung aus einer Grundfrequenz und vielen Mehrfachen dieser Frequenz. Die Amplitude der verschiedenen Mehrfachen bestimmt den Charakter des Signals.
 

Die FFT kann nun dazu benutzt werden, einen Ton wieder in seine Bestandteile zu zerlegen.
Sie kann aber auch das Signal-Rausch-Verhältnis eines Signals dramatisch verbessern.
 

FFT - kennt jeder

Ja wirklich. Man braucht nur auf eines der quitschbunt blinkenden Autoradiodisplays zu schauen oder Winamp zu starten, und schon bekommt man das Ergebnis einer FFT angezeigt. Bei Winamp ist es z.B. die flackernde Balkengrafik (im Bild über dem Wort WHIPPIN). Mit einer FFT kann man also analysieren, welche Frequenzanteile in einem Signal wie stark vertreten sind.

Ich verwende die FFT z.B. in meinen Programmen zur Geschwindigkeitsberechnung von Modellflugzeugen:

• WaveOscope
• VSpectrum

• HM-FFT

Die FFT als Filter-Bank

Die FFT ist ein Vorgang, bei dem man ein Signal in seine Bestandteile (also seine verschiedenen Frequenzen) zerlegt. Am ehesten kann man sich die FFT als ein Set von vielen Frequenzfiltern vorstellen. Alle Filter haben die gleiche Bandbreite, und einen gleichmäßigen Abstand. Sie decken lückenlos den Frequenzbereich von 0 Hz bis zu einer Maximalfrequenz ab. Mit 200 Filtern, die jeweils 100 Hz breit sind, kann man den gesamten Audio-Frequenzbereich von 0 Hz bis 20 kHz lückenlos abdecken. (Die Winamp-FFT hat geradeeinmal ca. 20 Filter, die natürlich alle deutlich breiter als 100 Hz sind.)

200 Filter wären als Hardware-Lösung schon recht aufwendig. Die FFT ist aber nur Software. So hat sie zwar kein Gewicht, verschlingt aber einiges an Rechenpower.
 

FFT ohne Mathematik erklärt

Mancher mag  mich dafür verfluchen wollen, aber ich will trotzdem mal versuchen, die FFT ganz mathematikfrei zu erklären.
 

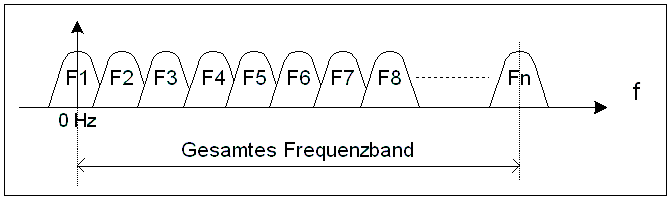Eine FFT  ist ein Set von Frequenzbandpässen (Filtern), die alle die gleiche Bandbreite und einen gleichmäßigen Abstand (=Bandbreite) haben. Zusammen decken sie ein bei 0 Hz beginnendes Frequenzband ab. Wird in den Eingang der Filterbank ein Signal mit einer bestimmten Frequenz eingespeist, dann erzeugt das zugehörige Filter ein starkes Ausgangssignal. Wird ein Frequenzgemisch eingespeist, dann reagieren mehrere Filter gleichzeitig.

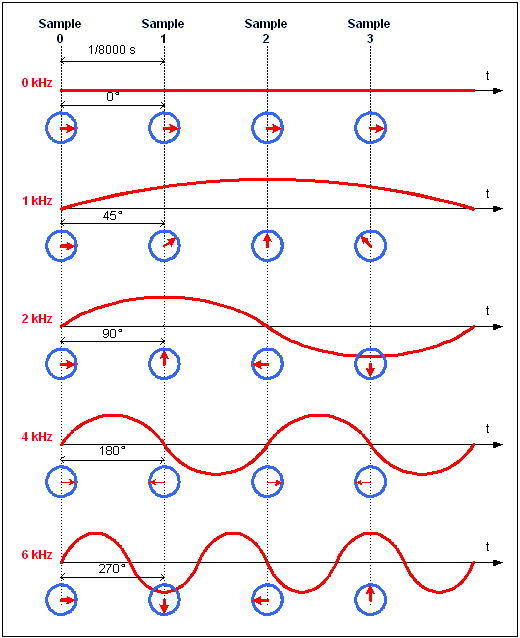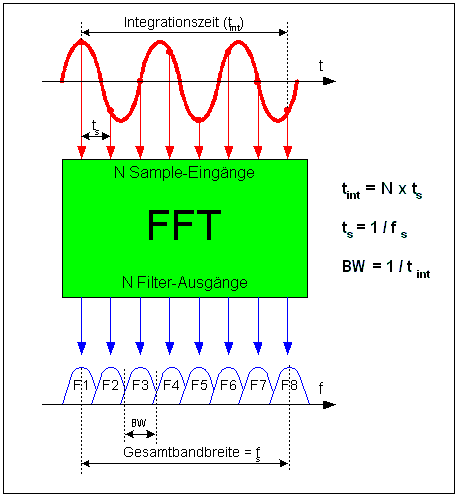
Das Eingangssignal der Filterbank Das Eingangssignal für eine FFT sind Samples des analogen Eingangssignals. Im nebenstehenden Beispiel habe ich einen 8-kHz -ADC benutzt, um verschiedene beispielhafte Eingangssignale zu wandeln. Es wurden jeweils 4 Samples genommen. Das Ergebnis sind die kleinen roten Pfeile. Die Länge des Pfeils entspricht der Signalstärke, die Richtung des Pfeils entspricht der momentanen Phase des Signals. Man sieht, dass sich von Sample zu Sample die Phase des gemessenen Eingangssignals bei jeder Frequenz unterschiedlich schnell ändert. Bei 0 kHz (DC) ist die Phase konstant, bei 1 kHz ändert sie sich immer um 45° bei 2 kHz um 90° ... Diese Phasenänderungen werden in einem Frequenzfilter verwendet, um die Frequenz des Eingangssignals zu bestimmen.   Die hier gezeigten Samples dienen nur der Veranschaulichung. Normalerweise habe ich ein mir unbekanntes Eingangssignal, das meist ein Gemisch verschiedenster Frequenzen ist.

Wie kann man den  nun überhaupt ein Frequenzfilter aufbauen? Hier sehen wir ein einfaches 1 kHz-Filter, das (so ein Zufall) gerade mit den 4 Samples eines 1-kHz-Signals gespeist wird. Das Filter besteht aus drei Phasendrehern und einer Summierstufe. Die Samples Nr 1..3 werden durch die Phasendreher geschickt. Dort wird ihre Phase um -45°, -90° bzw. -135° gedreht (geschoben). Danach werden alls Samples zusammenaddiert. Da  es sich um Samples eines 1-kHz-Signals handelte, waren sie untereinander um jeweils 45° phasenverschoben. Durch die Phasenrotatoren sind nun alle Samples gleichphasig. werden sie nun (vektoriell) addiert, erhält man eine große Summe, deren Amplitude dem Vierfachen der Eingangssignalamplitude entspricht.

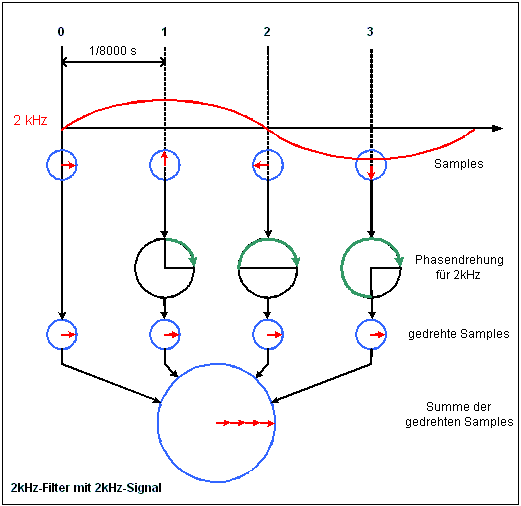Noch ein Frequenzfilter: Hier sehen wir ein einfaches 2 kHz-Filter, das (so ein Zufall) gerade mit den 4 Samples eines 2-kHz-Signals gespeist wird.  Die Samples Nr 1..3 werden durch die Phasendreher geschickt. Dort wird ihre Phase um -90°, -180° bzw. -270° gedreht (geschoben). Danach werden alls Samples zusammenaddiert. Da  es sich um Samples eines 2-kHz-Signals handelte, waren sie untereinander um jeweils 90° phasenverschoben. Durch die Phasenrotatoren sind nun alle Samples gleichphasig. werden sie nun (vektoriell) addiert, erhält man eine große Summe, deren Amplitude dem Vierfachen der Eingangssignalamplitude entspricht.

Nun füttern wir mal das 1 kHz-Filter mit einem 2-kHz-Signal. Die Samples sind untereinander jeweils um 90°  phasenverschoben. Die Phasendreher des 1-kHz-Filter drehen die Phasen aber nur um die Hälfte dieser Werte zurück.  Folglich sind die Samples nach den Phasendrehern nicht gleichphasig. Werden sie nun (vektoriell) zusammenaddiert, so ist die Amplitude der Summe deutlich kleiner (blauer Kreis) als wenn Filter und Frequenz  zusammenpassen würden (schwarzer Kreis).

Dieses Diagramm  zeigt die Ausgangsamplitude unseres 2-kHz-Filters für verschiedene Frequenzen. Man sieht deutlich das Maximum bei 2 kHz und die abnehmende Amplitude zu höheren und niedrigeren Frequenzen. Bei 1 kHz beträgt die Ausgangsamplitude etwa 2,5-Eingangsamplituden. Das deckt sich mit der obigen Grafik.

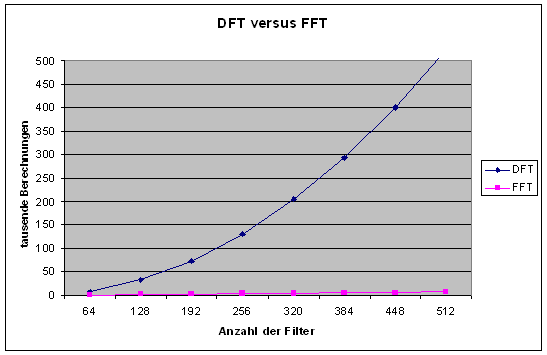
In der Praxis wissen wir natürlich nicht, welche Frequenz das Eingangssignal hat. Wir wollen das aber herausfinden. Dafür benötigen wir ein Set von verschiedenen Filtern, das die gleichen Eingangssamples parallel überprüft. Im nebenstehenden Bild sind 4 Filter eingetragen, die die gleichen 4 Samples auf die Frequenzen 0 kHz, 2 kHz, 4 kHz und 6 kHz hin überprüfen.  Die Keise mit dem P-Symbol sind Phasendreher (ich hatte keinen Platz um die jeweilige Phasenschiebung in Grad anzugeben) und die Kreise mit dem S-Symbol sind Summierer.  Das uns schon bekannte 2-kHz-Filter ist auch dabei.

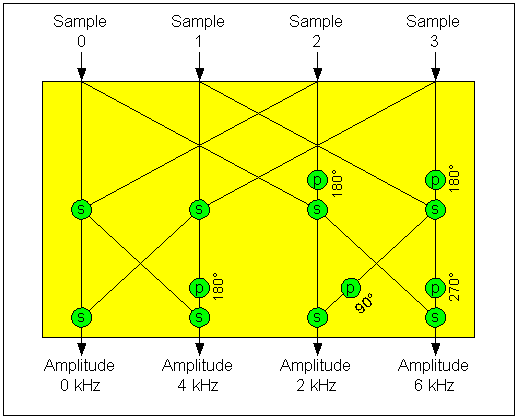
Mann könnte das zwar alles in Hardware realisieren, aber üblicherweise wird die Filterbank in Software erstellt. Folglich sind alle diese Phasendrehungen und Vektor-Summationen Berechnungen im Prozessor. Für ein paar Filter ist die Rechenlast noch gering, aber die dunkelblaue Linie in der nebenstehenden Grafik zeigt, wie schnell die Zahl der nötigen Berechnungen ansteigt, wenn man eine größere Zahl an Filtern benötigt. Die rote Linie sieht da doch viel beruhigender aus. Sie zeigt die Zahl der Berechnungen für eine FFT an. Die FFT ist eine vereinfachte Filterbank, die eine viel schnellere Berechnung möglich macht.

Diese Grafik zeigt unsere 4 Filter in einer FFT. Die Beschleunigung des Rechenverfahrens beruht darauf, dass man einige Phasendreher und einige Summatoren gleichzeitig für mehrere Filter benutzt. Es werden Zwischenergebnisse der Berechnung also mehrfach verwendet.  Schon diese 4-Filter-Bank hat einige Phasendreher und einige Summatoren weniger als das obere Beispiel mit gleichwertigen Filtern. Die Filter sind nun aber auch untereinander abhängig. Ich kann das 2-kHz-Filter n icht einfach so ändern, das es ein 2,5-kHz-Filter wird, da ich dann auch Phasendreher des 6-kHz-Filters verändern müsste... Es gibt deshalb für die FFT einige feste Regeln: Alle Filter haben die gleiche Bandbreite. Alle Filter liegen in gleichmäßigen Frequenzabständen. Die Zahl der Filter ist eine Zweierpotenz (4, 8, 16, 32, 64, 128, ...). Die Zahl der Samples ist gleich der Zahl der Filter.

Wir können sehen, das die Berechnung unserer 4-Filter-FFT in 2 Stufen abläuft. Nur dadurch fallen überhaupt Zwischenergebnisse an, die mehrfach genutzt werden können. FFTs mit mehr Filtern (8, 16, 32 ...) laufen in noch mehr Stufen ab (3, 4, 5 ...) wodurch Zwischenergebnisse noch häufiger benutzt werden können. Dadurch steigt die Effizienz der FFT im Vergleich zur einfachen Filterbank.

Natürlich wird dabei das im obrigen Bild zu sehende Netzwerk (Butterfly) noch um einiges komplexer.  

Für eine FFT gibt es einige feste Zusammenhänge zwischen Frequenzen und Bandbreiten. Die FFT wird mit N Messwerten gefüttert, die Samples des unbekannten Eingangssignals (rot) sind. Die Samples wurden (vom ADC) mit einem festen Abstand ts gemessen. Dieser Abstand ist das Reziprok der ADC-Samplefrequenz. Die Zahl der Samples  (N) ist eine Potenz von 2. Im nebenstehenden Bild ist N=8, es könnte aber auch z.B. 1024 sein. Die Anzahl der von der FFT erzeugten Filter (blau) ist ebenfalls N. Die Zeit vom ersten bis zum letzten Sample ist die Integrationszeit tint der FFT. Sie ist für die Bandbreite der einzelnen FFT-Filter zuständig. Eine lange Integrationszeit führt zu schmaleren Filtern. Die Filterbandbreite (BW) ist das Reziprok der Integrationszeit. Die Gesamtbandbreite aller FFT-Filter zusammen ist gleich der Samplefrequenz fs des ADC.    Beispiel 1: Eine FFT wird mit 512 Samples eines 8-kHz-ADC gespeist. Daraus folgt: Die FFT hat 512 Filter. Jeder Filter ist 15,625 Hz breit.  (8 kHz / 512) Beispiel 2: Eine FFT wird mit 128 Samples eines 8-kHz-ADC gespeist. Daraus folgt: Die FFT hat 128 Filter. Jeder Filter ist 62,5 Hz breit.

Komplexe Zahlen / IQ / Sinus & Cosinus

Wer sich mit der FFT näher beschäftigt, wird zwangsläufig auf komplexe Zahlen stoßen. Wozu werden die benötigt?

Die FFT rechnet mit Phasen von Signalen, also mit den netten kleinen roten Pfeilen aus der obrigen Beschreibung. Prozessoren rechnen aber mit Zahlen. Diese Pfeile lassen sich leider nicht mit einer einzelnen Zahl beschreiben, man benötigt zwei Zahlen.
 

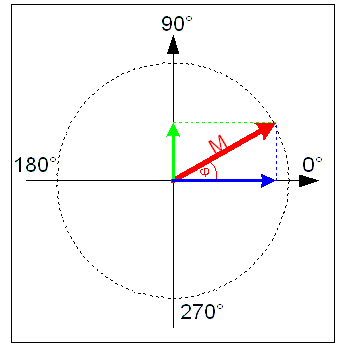So könnte man mit jeweils einer Zahl die Länge des Pfeils (Amplitude M) und mit der anderen die Richtung (Phase phi = j) beschreiben. Üblicher ist es aber die Projektionen des Pfeiles in einem rechtwickligen Koordinatensystem zu verwenden. Das ist in dieser Grafik dargestellt. Durch die Projektion des roten Pfeiles (M) erhält man einen blauen und einen grünen Pfeil auf den Koordinatenachsen. Da deren Richtung bekannt ist (entlang den Koordinatenachsen) braucht man sich nur die Länge dieser Pfeile zu speichern. Diese beiden Zahlen enthalten dann zusammen die Phase und die Länge des Pfeils. Das Zahlenpaar ist nun also ein Vector, und man muss sich noch nette Namen für die beiden Zahlen einfallen lassen. Mathematiker kennen bereits Zahlen mit zwei unabhängigen Komponenten: die komplexen Zahlen mit ihrem realen und imaginären Anteilen. So wird das Zahlenpaar gern als komplexe Zahl bezeichnet. Da es sich bei der Länge des grünen und blauen Pfeils aber um M x sin(phi)  und M x cos(phi) handelt, bezeichnet man sie manchmal auch als I und Q. Dabei steht I für Inphase-Komponente und Q für Quadratur-Komponente. Man kann auch sagen, dass Q um eine Viertelwelle (Quaterwave) zu I phasenverschoben ist. Es sind Sinus und Cosinus des Signals.

Phasenmessung?

Im der obigen FFT-Beschreibung, wird das Eingangssignal in kleine rote Pfeile gewandelt. Die Richtung der Pfeile entspricht der Phase des Eingangssignals. Wie misst man aber die Phase?
Wir können die Amplitude des Eingangssignals mit dem ADC in festen Abständen messen, dadurch wissen wir aber noch lange nicht die Phase des Signals am Messpunkt. Hier helfe ich mir manchmal mit einen (nicht ganz sauberen) Trick:
 

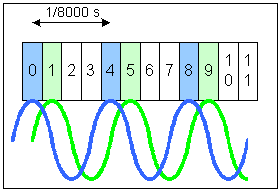Angenommen, der ADC arbeitet mit einer Samplefrequenz von 32 kHz (32 000 Samples/s). In 10 ms erhalten wir dann 320 Messwerte vom ADC, die ich von 0 bis 319 durchnummeriere. Die Messwerte 0, 4, 8, 12, 16 ... entsprechen dabei dem Zahlenstrom, den ein 8 kHz ADC geliefert hätte. Die Messwerte 1, 5, 9, 13, 17 ... könnten von einem zweite 8 kHz-ADC stammen, der im Vergleich zum ersten ADC um 90° phasenverschoben arbeitet. Damit hat man zwei Zahlenströme. Einer entspricht dem Sinus und der andere dem Cosinus des Eingangssignals bei einer Sampelrate von 8 kHz. Damit kann man immer Amplitude und Phase ermitteln. Die übrigen Messwerte (2, 3, 6, 7 ... ) wirft man weg. Das ist zwar ein wenig getrixt, und man hat nur noch 1/4 der ADC-Samplerate, meist reicht dass aber aus. Die Samplepaare 0&1  /  4&5  /  8&9 .. bilden also jeweils einen Vector (meinetwegen auch eine komplexe Zahl oder ein IQ-Paar) das als ein Sample für die FFT taugt. Von den 320 Samples bleiben also nur 80 Vectoren für die FFT übrig. Das reicht noch für eine 64-Filter breite FFT.

Ist die Frequenz des analogen Eingangssignals ohnehin zu groß für die Verarbeitung in einer FFT, dann kann man das Signal zunächst analog auf eine handliche Frequenz heruntermischen, und dabei auch gleich echtes I und Q erzeugen. Dazu verwendet man zwei parallele Mischer. Einer wird mit dem Sinus und der andere mit dem Cosinus der Mischfrequenz (LO-Frequenz) gespeist. Dadurch sind auch die beiden Mischerausgangssignale um 90° untereinander phasenverschoben. Die anderen Mischprodukte werden mit Tiefpassfiltern unterdrückt, und I und Q in zwei separaten ADCs parallel in Zahlenströme gewandelt.

Autor: sprut
erstellt am: 27.03.2006
letzte Änderung: 10.08.2009

Quellen: Nullsoft (für den Winamp-Screenshot)